公差は分類すると【寸法公差】【はめあい公差】【幾何公差】の3つに分けることができます。
今回はその中の【寸法公差】について解説していきます。
寸法公差とは?
寸法公差とは、寸法の誤差を表す数値です。
製品は指定した寸法値、その値ピッタリに出来上がることはありません。そのため、許容することができる範囲(最大/最小の許容寸法)を指定するために公差を記載します。
例えば、下図のような部品に対して寸法を考えてみます。
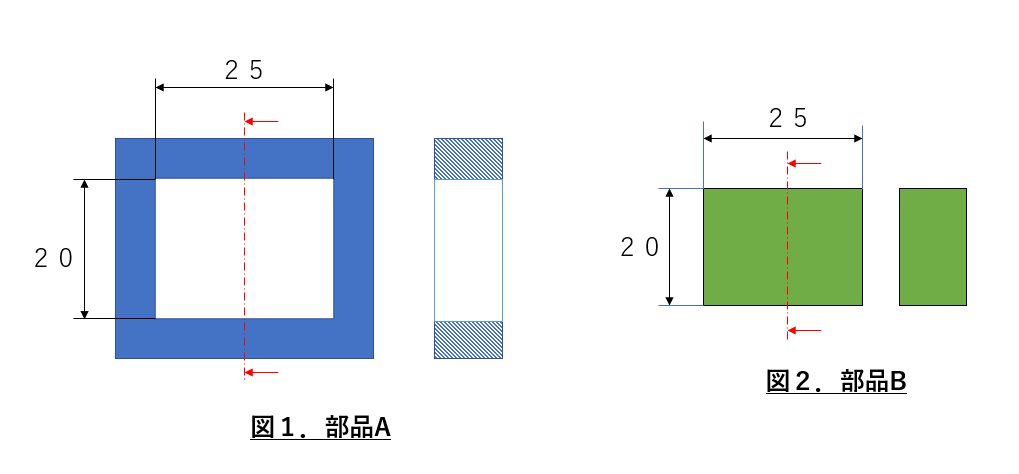
部品Aの「25mm×20mmの開口部へ部品Bを挿入する」場合、現状のままでは製品に誤差が生じてしまうと挿入ができなくなってしまうため、製作誤差を考慮し寸法公差を記載していきます。
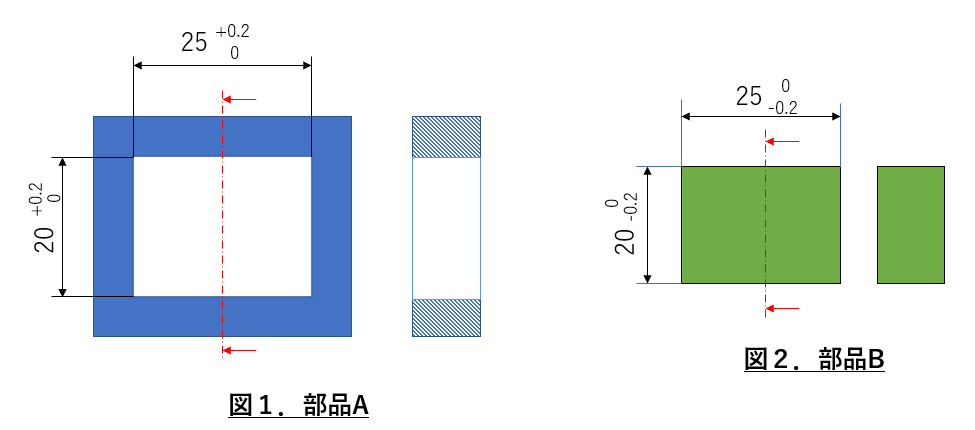
このように部品Bが部品Aの開口部より大きくならないよう公差(最大/最小の許容値)を記載します。
つまり公差とは、製品が設計の意図通りに組立つ、機能するよう記入する数値とも言えます。
図面にはどう記載する?
では、実際に図面にはどのように書いていくのでしょうか。
形状寸法へ直接記載する場合は、前途した通り寸法の隣へ最大/最小の許容値を記載してあげます。最大の寸法を上、最小の寸法を下へ記載するのがルールです。
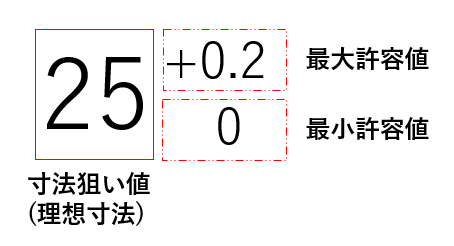
寸法の隣へ直接記載する公差の他にもJISで規定される【普通公差】とよばれる公差もあります。この公差は、寸法の隣への記載はしません。なぜなら図面内に公差記載のない全ての寸法に適用されるからです。【普通公差】の多くは図面へ下記のような形で記載されています。
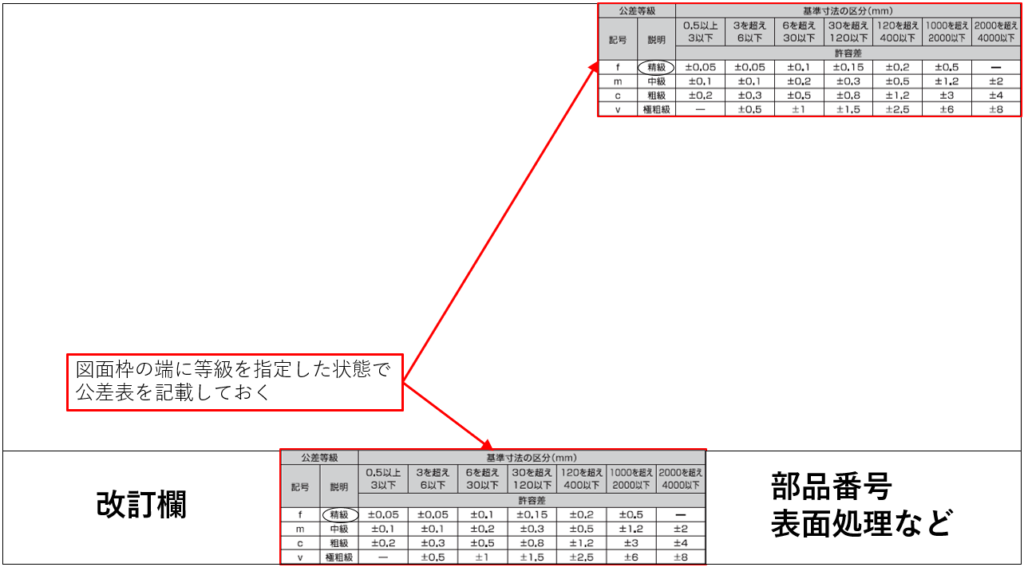
普通公差は加工/製作方法毎に異なります。今回は削り加工における公差を引用して記載しています。
一部をご紹介しておきます。興味のある方はJISを調べてみて下さい。
- 削り加工:JIS B 0405
- 金属プレス加工:JIS B 0408
- 鋳物:JIS B 0403
公差の考え方|応用例 二乗平均
ここまで寸法公差について基礎をご紹介してきました。
ここからは、実際に製品設計を行う際に使用する手法/考え方の応用例「二乗平均」をご紹介します。
現在、世の中に出回っている工業製品のほとんどは複数の部品を組立てることで成り立っています。その複数の部品が組み合わさる時に使用する公差の考え方です。
具体的に簡単な例を用いて計算していきます。
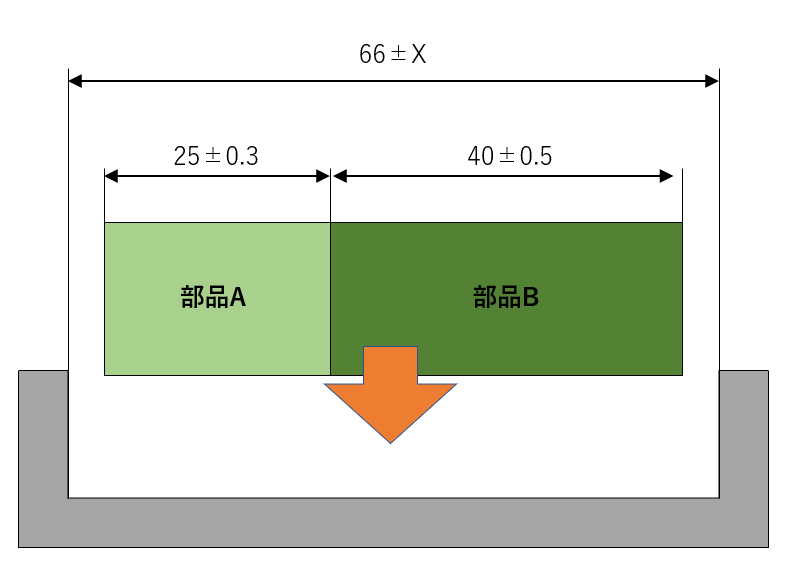
こうのような組合せの製品で考えていきます。今部品Aと部品Bをコの字型の容器へ挿入しようとしています。この際、部品Aと部品Bには上手の通り寸法と公差が設定されているものとします。
その場合に容器の寸法公差『X』の値をいくつに設定すれば、トラブルなく製品を組立てることができるか、その検討を行う際に二乗平均を用いていきます。
二乗平均の考え方を用いるための条件
ただし二乗平均の考え方を用いるには条件があります。その条件とは、
加工してできる寸法ばらつきが正規分布に従い、その標準偏差σが「平均値±3σの領域に99.7%入っている場合」です。簡単に言うと、工程能力が十分に確保できている場合(=きちんと公差内で部品を製作できる場合)ということです。
標準偏差とは?など詳しい話はまた別で解説しますね。今回は二乗平均の考え方を使用するにはこんな条件があるんだぁってくらいで覚えておいて下さい。
二乗平均で計算する公差
実際に計算してみましょう。

部品Aと部品Bをコの字型の容器に入れる場合、単純に66mmの容器に65mmの部品を入れるので隙間は1mmとなります。全ての公差の最小値が1mmを超えなければ問題なく組立てることができるので、
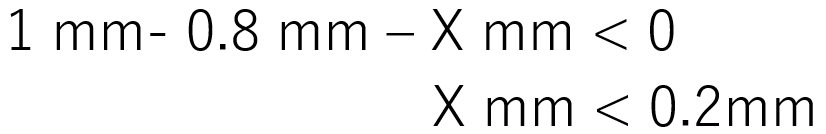
Xの値が0.2mm以下であれば、製品が成り立つことが分かります。
ですが、二乗平均で考えると以下のようになります。
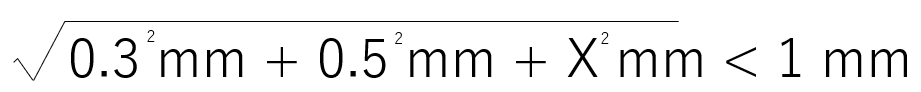
上式を計算すると、X<0.8124となりますので単純に計算した場合に比べ倍以上の公差を設定することができ、製作時の寸法不良を減らすことが出来ます。
以上が二乗平均による公差の考え方です。
簡単ではありませんが、覚えておくと設計の際に役に立つ知識はであると思いますので、是非覚えてみて下さい。今回は簡単に公差設定のやり方のみご紹介しました。
なぜ二乗平均が成り立つのか、その理由などはまた別の記事で解説していきますので、是非参考にしてみて下さい。



コメント